1890번: 점프
첫째 줄에 게임 판의 크기 N (4 ≤ N ≤ 100)이 주어진다. 그 다음 N개 줄에는 각 칸에 적혀져 있는 수가 N개씩 주어진다. 칸에 적혀있는 수는 0보다 크거나 같고, 9보다 작거나 같은 정수이며, 가장
www.acmicpc.net
처음에는 다음과 같이 BFS로 풀었다. 하지만 메모리초과가 났다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <tuple>
using namespace std;
int main() {
cin.tie(NULL);
ios::sync_with_stdio(false);
int n;
cin >> n;
vector<vector<int>> v(n, vector<int>(n));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> v[i][j];
}
}
vector<vector<long long>> answer(n, vector<long long>(n, 0));
queue <pair<int, int>> q;
q.push(make_pair(0, 0));
while (!q.empty()) {
pair<int, int> cur = q.front();
q.pop();
int row = cur.first;
int col = cur.second;
if (v[row][col] == 0)
continue;
if (row + v[row][col] < n) {
if (row + v[row][col] != n - 1 || col != n - 1) {
q.push(make_pair(row + v[row][col], col));
}
answer[row + v[row][col]][col]++;
}
if (col + v[row][col] < n) {
if (row != n - 1 || col + v[row][col] != n - 1) {
q.push(make_pair(row, col + v[row][col]));
}
answer[row][col + v[row][col]]++;
}
}
cout << answer[n - 1][n - 1];
return 0;
}
그래서 DP로 풀었다.
초등학교 고학년 때인지 중학교 때인지 다음과 같은 그림을 주면서
'출발점에서 도착점으로 가는 최단경로의 개수를 구하시오'
하는 문제 본 적 있을 것이다.
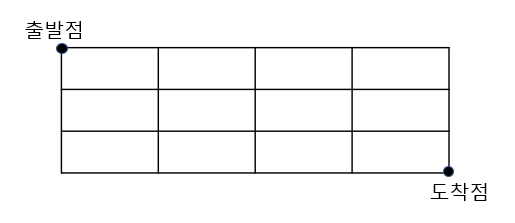
그 때 어떻게 풀었냐면
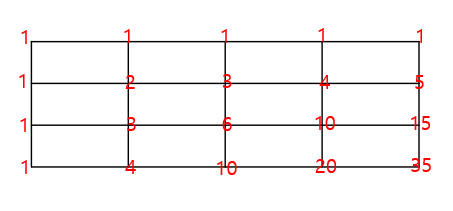
다들 이렇게 풀었을 것이다.
설명을 하자면
최단경로이므로 아래쪽 또는 오른쪽으로만 이동해야 한다.
따라서 위, 왼쪽의 숫자를 더한 것이 출발점에서 현 지점까지 오는 최단경로의 개수이다.
이것을 계속 반복하면 도착점까지의 최단경로의 개수를 구할 수 있다.
1890번 문제도 똑같다. 최단경로라는 말은 없지만 반드시 오른쪽이나 아래쪽으로만 이동해야 한다는 조건이 있다.
다만 거리가 이동 거리가 무조건 1이 아니라 특정 숫자만큼만 점프를 할 수 있다는 것 뿐이다.
입력으로
4
2 3 3 1
1 2 1 3
1 2 3 1
3 1 1 0이렇게 들어왔다고 하자.
입력값으로 들어온 것은 벡터 v에 저장해주고 동적계획법으로 풀 때 값들을 저장할 벡터는 answer이라고 했다.
초기상태는 다음과 같다.
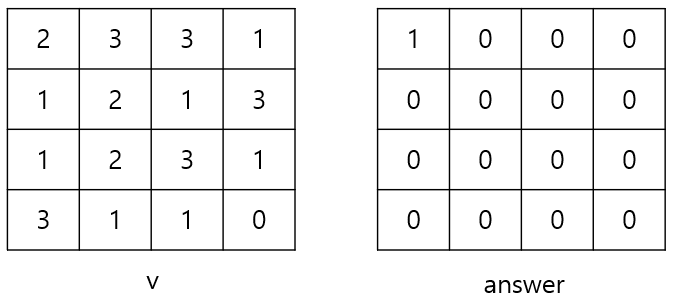
v는 입력받은 것이고 answer[0][0]은 1을 저장해주었다.
i = 0, j = 0일 때

위쪽과 왼쪽으로 가볼 곳이 없다.
i = 0, j = 1일 때
k = 1이면
한 칸 왼쪽으로 가보면 v[0][0]은 1이 아니라 2이므로 안 된다.
왜 안 되냐? v에 저장된 값은 '몇 칸 점프할 수 있는지'이다. 따라서 v[0][0]은 2이므로 0행 0열에서는 두 칸 점프할 수 있다. 그런데 0행 0열에서 두 칸 점프해서는 0행 1열에 도달할 수 없다. 한 칸 점프해야만 도달할 수 있다. 즉 v[0][0]이 1일 때만 가능하다.

i = 0, j = 2일 때
k = 1이면
한 칸 왼쪽으로 가보면 v[0][1]은 1이 아니라 3이므로 안 된다.
k = 2이면
두 칸 왼쪽으로 가보면 v[0][0]은 2이므로 answer[0][0] 만큼을 더해준다. 즉, 1을 더해준다.

i = 0, j = 3일 때
k = 1이면
한 칸 왼쪽으로 가보면 v[0][1]은 1이 아니라 3이므로 안 된다.
k = 2이면
두 칸 왼쪽으로 가보면 v[0][1]은 2가 아니라 3이므로 안 된다.
k = 3이면
세 칸 왼쪽으로 가보면 v[0][1]은 3이 아니라 2이므로 안 된다.

i = 1, j = 0일 때
k = 1이면
한 칸 위쪽으로 가보면 v[0][0]은 1이 아니라 2이므로 안 된다.

i = 1, j = 1일 때
k = 1이면
한 칸 위쪽으로 가보면 v[0][1]은 1이 아니라 3이므로 안 된다.
한 칸 왼쪽으로 가보면 v[1][0]은 1이므로 answer[1][0] 만큼을 더해준다. 즉, 0을 더해준다.

i = 1, j = 2일 때
k = 1이면
한 칸 위쪽으로 가보면 v[0][2]은 1이 아니라 3이므로 안 된다.
한 칸 왼쪽으로 가보면 v[1][1]은 1이 아니라 2이므로 안 된다.
k = 2이면
두 칸 왼쪽으로 가보면 v[1][0]은 2가 아니라 1이므로 안 된다.
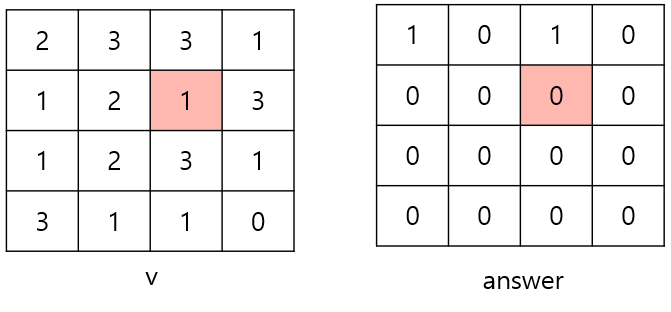
i = 1, j = 3일 때
k = 1이면
한 칸 위쪽으로 가보면 v[0][3]은 1이므로 answer[0][3] 만큼을 더해준다. 즉, 0을 더해준다.
한 칸 왼쪽으로 가보면 v[1][2]은 1이므로 answer[1][2] 만큼을 더해준다. 즉, 0을 더해준다.
k = 2이면
두 칸 왼쪽으로 가보면 v[1][1]은 2이므로 answer[1][1] 만큼을 더해준다. 즉, 0을 더해준다.
k = 3이면
세 칸 왼쪽으로 가보면 v[1][0]은 3이 아니라 1이므로 안 된다

i = 2, j = 0일 때
k = 1이면
한 칸 위쪽으로 가보면 v[1][0]은 1이므로 answer[1][0] 만큼을 더해준다. 즉, 0을 더해준다.
k = 2이면
두 칸 위쪽으로 가보면 v[0][0]은 2이므로 answer[0][0] 만큼을 더해준다. 즉, 1을 더해준다.
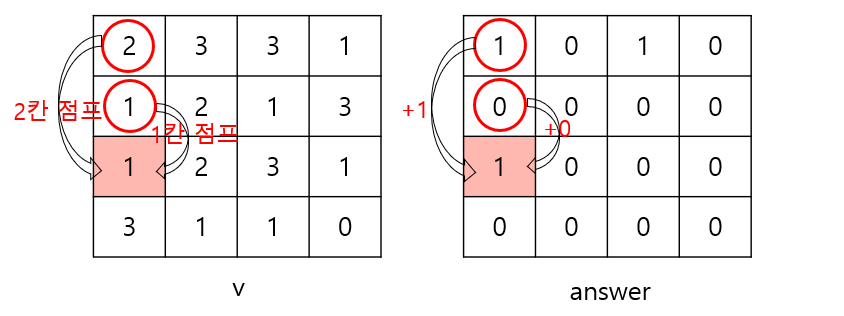
i = 2, j = 1일 때
k = 1이면
한 칸 위쪽으로 가보면 v[1][1]은 1이 아니라 2이므로 안 된다.
한 칸 왼쪽으로 가보면 v[2][0]은 1이므로 answer[2][0] 만큼을 더해준다. 즉, 1을 더해준다.
k = 2이면
두 칸 위쪽으로 가보면 v[0][1]은 2가 아니라 3이므로 안 된다.

i = 2, j = 2일 때
k = 1이면
한 칸 위쪽으로 가보면 v[1][2]는 1이므로 answer[1][2] 만큼을 더해준다. 즉, 0을 더해준다.
한 칸 왼쪽으로 가보면 v[2][0]은 1이 아니라 2이므로 안 된다.
k = 2이면
두 칸 위쪽으로 가보면 v[0][2]은 2가 아니라 3이므로 안 된다.
두 칸 왼쪽으로 가보면 v[2][0]은 2가 아니라 1이므로 안 된다.

i = 2, j = 3일 때
k = 1이면
한 칸 위쪽으로 가보면 v[2][0]은 1이 아니라 3이므로 안 된다.
한 칸 왼쪽으로 가보면 v[2][0]은 1이 아니라 3이므로 안 된다.
k = 2이면
두 칸 위쪽으로 가보면 v[2][0]은 2가 아니라 1이므로 안 된다.
두 칸 왼쪽으로 가보면 v[2][1]은 2이므로 answer[2][1] 만큼을 더해준다. 즉, 1을 더해준다.
k = 3이면
세 칸 왼쪽으로 가보면 v[2][0]은 3이 아니라 1이므로 안 된다.
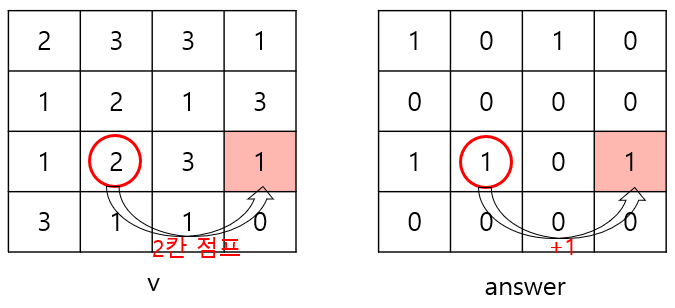
i = 3, j = 0일 때
k = 1이면
한 칸 위쪽으로 가보면 v[2][0]은 1이므로 answer[2][0] 만큼을 더해준다. 즉, 1을 더해준다.
k = 2이면
두 칸 위쪽으로 가보면 v[1][0]은 2가 아니라 1이므로 안 된다.
k = 3이면
세 칸 위쪽으로 가보면 v[0][0]은 3이 아니라 2이므로 안 된다.

i = 3, j = 1일 때
k = 1이면
한 칸 위쪽으로 가보면 v[2][1]은 1이 아니라 2이므로 안 된다.
한 칸 왼쪽으로 가보면 v[3][0]은 1이 아니라 3이므로 안 된다.
k = 2이면
두 칸 위쪽으로 가보면 v[1][1]은 2이므로 answer[1][1] 만큼을 더해준다. 즉, 0을 더해준다.
k = 3이면
세 칸 위쪽으로 가보면 v[0][1]은 3이므로 answer[0][1] 만큼을 더해준다. 즉, 0을 더해준다.
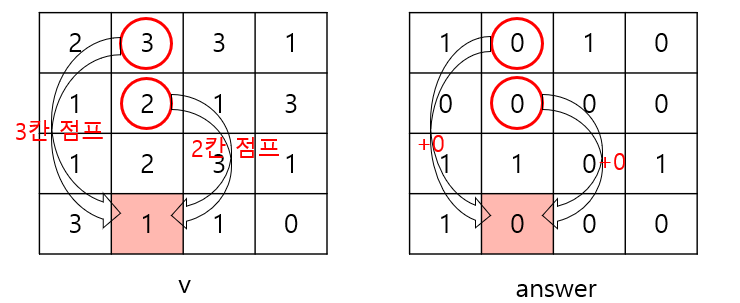
i = 3, j = 2일 때
k = 1이면
한 칸 위쪽으로 가보면 v[2][2]은 1이 아니라 3이므로 안 된다.
한 칸 왼쪽으로 가보면 v[3][1]은 1이므로 answer[3][1] 만큼을 더해준다. 즉, 0을 더해준다.
k = 2이면
두 칸 위쪽으로 가보면 v[1][2]은 2가 아니라 1이므로 안 된다.
두 칸 왼쪽으로 가보면 v[3][0]은 2가 아니라 3이므로 안 된다.
k = 3이면
세 칸 위쪽으로 가보면 v[0][2]은 3이므로 answer[0][2] 만큼을 더해준다. 즉, 1을 더해준다.
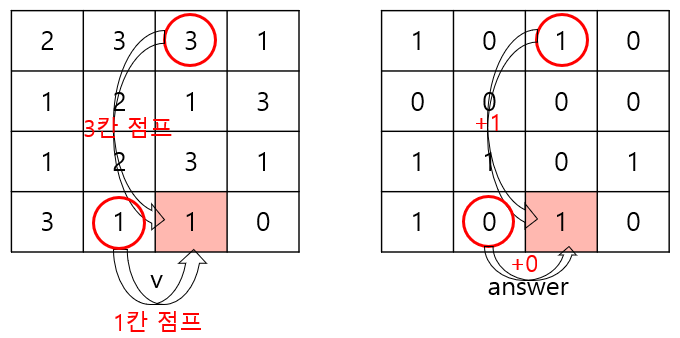
i = 3, j = 3일 때
k = 1이면
한 칸 위쪽으로 가보면 v[2][3]은 1이므로 answer[2][3] 만큼을 더해준다. 즉, 1을 더해준다.
한 칸 왼쪽으로 가보면 v[3][2]은 1이므로 answer[3][2] 만큼을 더해준다. 즉, 1을 더해준다.
k = 2이면
두 칸 위쪽으로 가보면 v[1][3]은 2가 아니라 3이므로 안 된다.
두 칸 왼쪽으로 가보면 v[3][1]은 2가 아니라 1이므로 안 된다.
k = 3이면
세 칸 위쪽으로 가보면 v[0][3]은 3이 아니라 1이므로 안 된다..
세 칸 왼쪽으로 가보면 v[3][0]은 3이므로 answer[3][0] 만큼을 더해준다. 즉, 1을 더해준다.

이해가 안 간다면 다음 동영상을 참고하면 된다. (혼을 갈아서 만든 영상입니다..)
#include <iostream>
#include <vector>
using namespace std;
int main() {
cin.tie(NULL);
ios::sync_with_stdio(false);
int n;
cin >> n;
vector<vector<int>> v(n, vector<int>(n));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> v[i][j];
}
}
vector<vector<long long>> answer(n, vector<long long>(n, 0));
answer[0][0] = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 1; k <= i; k++) {
if (v[i - k][j] == k) {
answer[i][j] += answer[i - k][j];
}
}
for (int k = 1; k <= j; k++) {
if (v[i][j - k] == k) {
answer[i][j] += answer[i][j - k];
}
}
}
}
cout << answer[n - 1][n - 1];
return 0;
}
'알고리즘 문제' 카테고리의 다른 글
| [백준] 11725번 트리의 부모 찾기 (0) | 2021.01.14 |
|---|---|
| [백준] 2960번 에라토스테네스의 체 (0) | 2021.01.14 |
| [백준] 1676번 팩토리얼 0의 개수 (0) | 2021.01.13 |
| [백준] 1107번 리모컨 (0) | 2021.01.11 |
| [백준] 1013번 Contact (0) | 2021.01.08 |
