[백준] 1915번 가장 큰 정사각형
1915번: 가장 큰 정사각형
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다.
www.acmicpc.net
당연히 브루트포스로 하면 시간초과가 날 것이므로 DP로 접근하였다.
char 타입의 벡터 v에 입력을 받고 벡터 dp를 선언하여 정답을 구했다.
벡터 v와 벡터 dp의 크기는 n행 m열로 선언한 것이 아니라 다음과 같이 n+1행 m+1열로 선언했다. (n = 4, m = 4일 때)
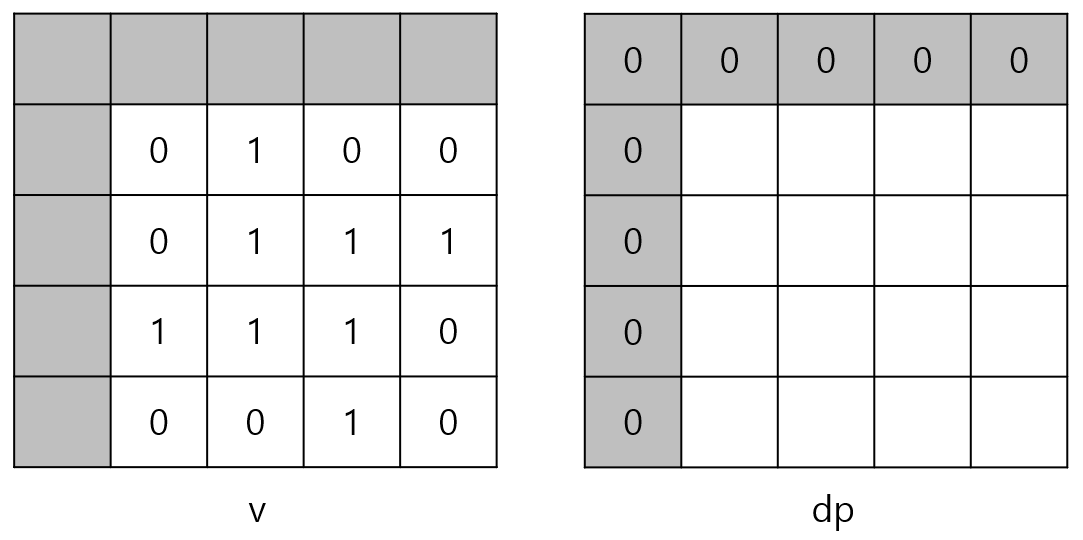
그 이유는 dp[i - 1][j - 1], dp[i][j - 1], dp[i - 1][j] 이런 식으로 현재 인덱스 - 1을 해줄 때 i - 1 >= 0인지, j - 1 >= 0인지 조건을 체크해줄 필요가 없어서 편하기 때문이다.
dp[i][j]에는 i행 j열을 오른쪽 아래 꼭짓점으로 하는 정사각형의 변의 길이를 저장해주었다.
v[i][j]가 0이면 1로 된 정사각형을 만들 수 없으므로 v[i][j]가 0이면 dp[i][j]는 반드시 0이다.
점화식은
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
이다.
점화식이 왜 이렇게 되는지는 다음 예시를 보면 이해가 갈 것이다.
예를 들어 입력으로
3 4
0110
1110
1110이렇게 들어온다면
벡터 v는 다음과 같을 것이다.
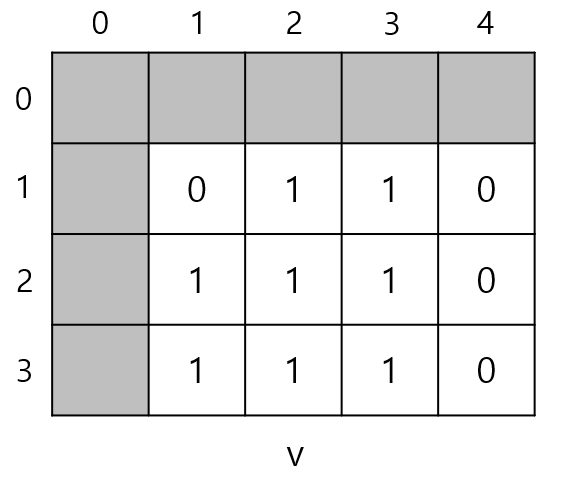
여기서 한 변의 길이가 2인 정사각형을 만들 수 있다.

빨간색 정사각형과 파란색 정사각형을 만들 수 있으므로 dp[2][3] = 2, dp[3][2] = 2가 된다.
그렇다면 dp[3][3]은 몇일까?

만약에 점화식이 dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1 이라면 dp[3][3]은 min(2, 2) + 1이므로 3이 된다.
과연 한 변의 길이가 3인 정사각형을 만들 수 있을까?
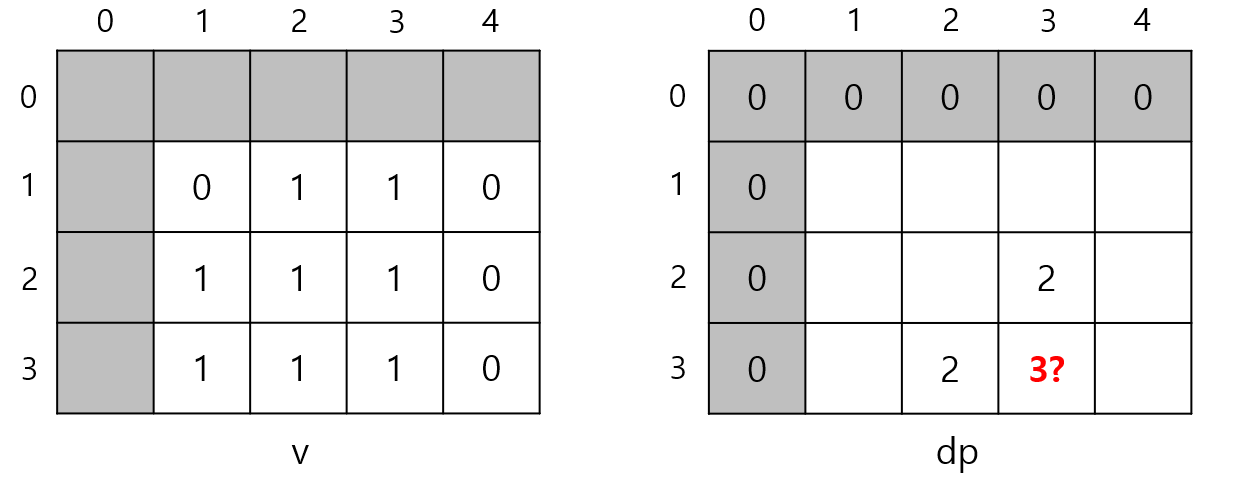
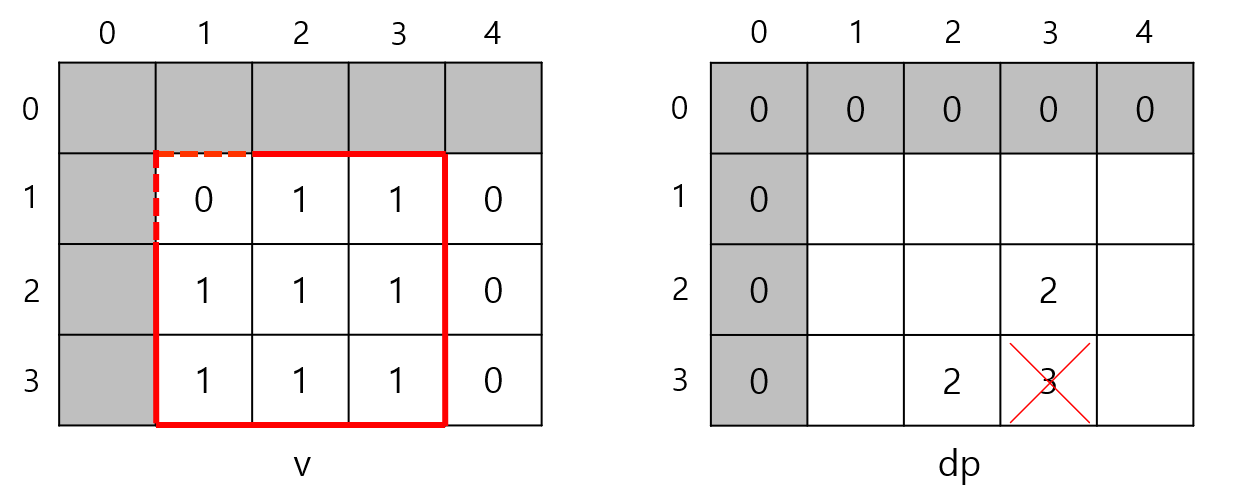
v[1][1]이 0이므로 변의 길이가 3인 정사각형은 만들 수 없다. 따라서 dp[3][3]은 3이 될 수 없다. v[2][2]가 1이기 때문이다.
dp[3][3]은 2가 되어야 한다.
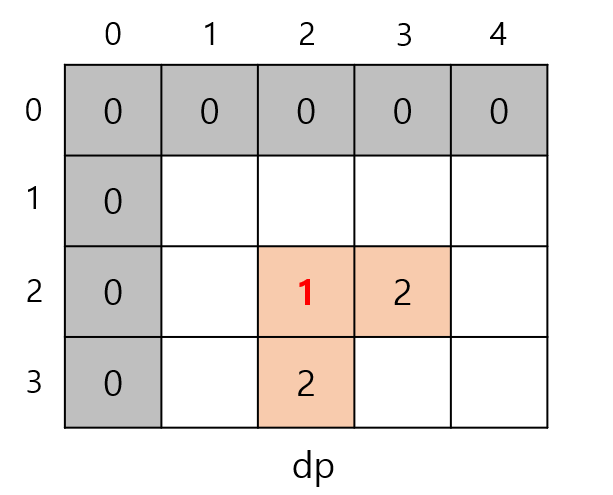

dp[2][2], dp[2][3], dp[3][2] 중 최솟값에 1을 더한 것이 dp[3][3]의 값 된다.
따라서 점화식은
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
가 된다.
예제와 같이 입력이 다음과 같이 들어온다면
4 4
0100
0111
1110
0010초기 상태의 v와 dp는 다음과 같다.

i = 1, j = 1일 때는 v[1][1]이 0이므로 dp[1][1]도 0이다.
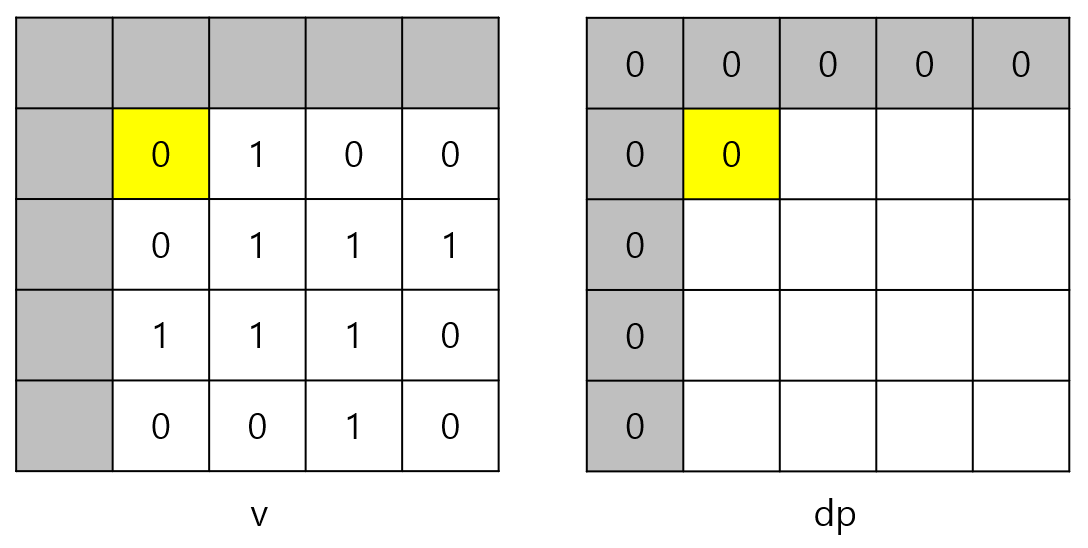
i = 1, j = 2일 때는 dp[0][0], dp[0][1], dp[1][0]의 최솟값이 0이므로
dp[1][2] = min(dp[0][0], dp[0][1], dp[1][0]) = 0 + 1 = 1이 된다.

i = 1, j = 3일 때는 v[1][3]이 0이므로 dp[1][3]도 0이다.
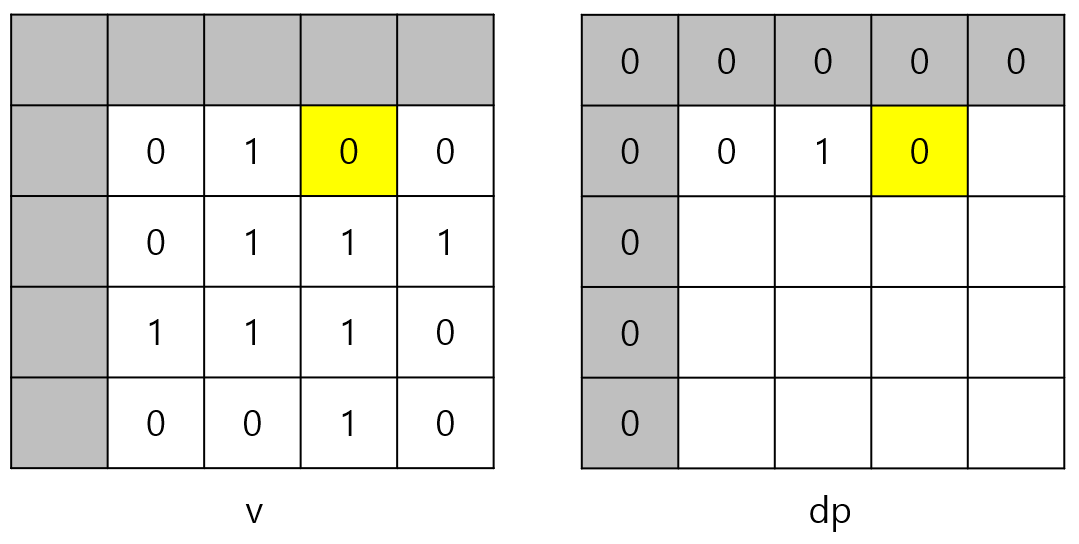
i = 1, j = 4일 때는 v[1][4]이 0이므로 dp[1][4]도 0이다.

i = 2, j = 1일 때는 v[2][1]이 0이므로 dp[2][1]도 0이다.

i = 2, j = 2일 때는 dp[1][1], dp[1][2], dp[2][1]의 최솟값이 0이므로
dp[2][2] = min(dp[1][1], dp[1][2], dp[2][1]) = min(0, 1, 0) + 1 = 0 + 1 = 1이 된다.
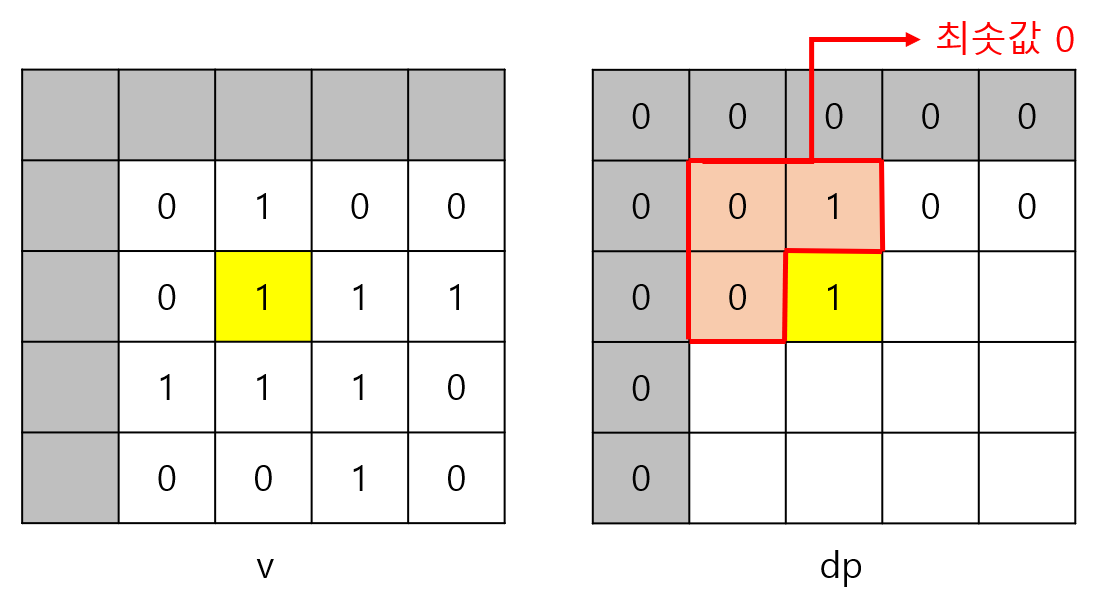
i = 2, j = 3일 때는 dp[1][2], dp[1][3], dp[2][2]의 최솟값이 0이므로
dp[2][3] = min(dp[1][2], dp[1][3], dp[2][2]) = min(1, 0, 1) + 1 = 0 + 1 = 1이 된다.

i = 2, j = 4일 때는 dp[1][3], dp[1][4], dp[2][3]의 최솟값이 0이므로
dp[2][4] = min(dp[1][3], dp[1][4], dp[2][3]) = min(0, 0, 1) + 1 = 0 + 1 = 1이 된다.
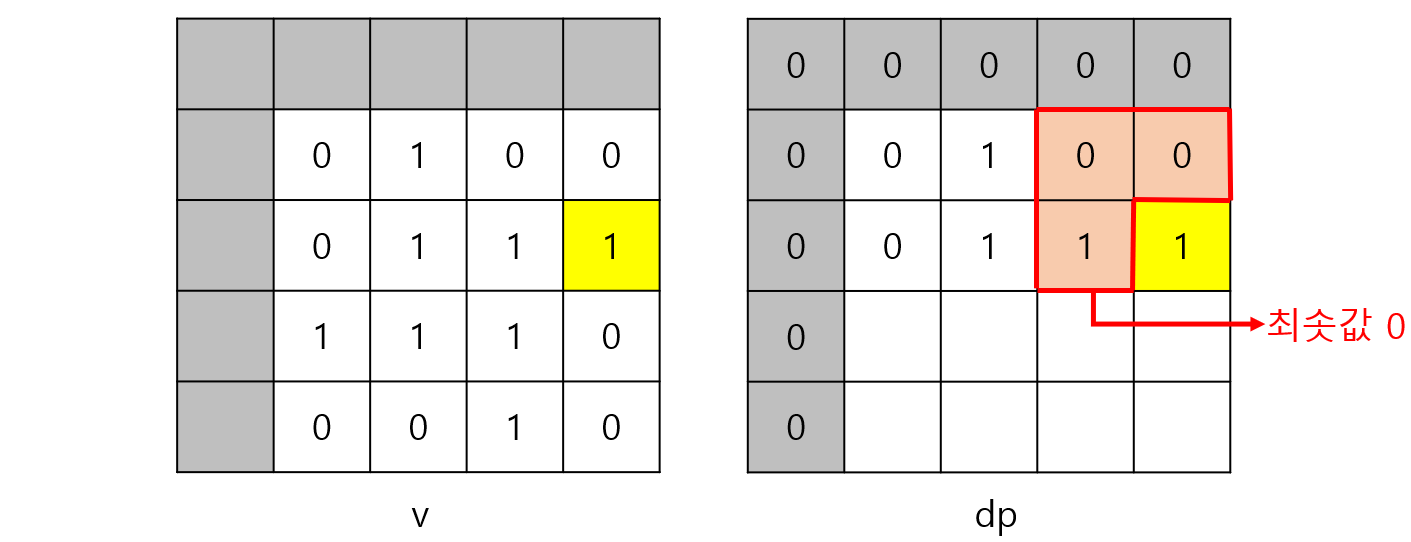
i = 3, j = 1일 때는 dp[2][0], dp[2][1], dp[3][0]의 최솟값이 0이므로
dp[3][1] = min(dp[2][0], dp[2][1], dp[3][0]) = min(0, 0, 0) + 1 = 0 + 1 = 1이 된다.

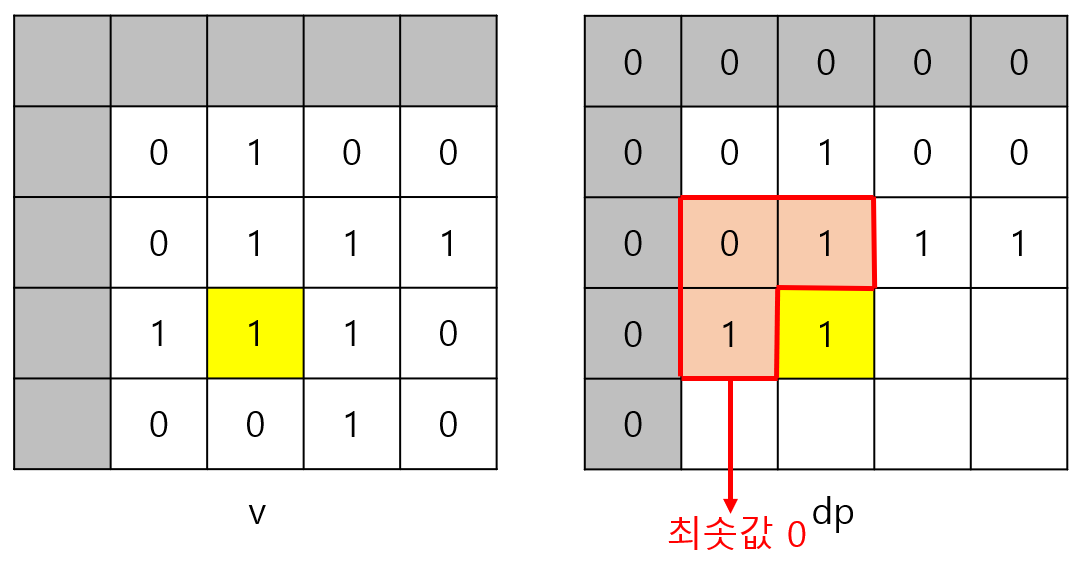
i = 3, j = 2일 때는 dp[2][1], dp[2][2], dp[3][1]의 최솟값이 0이므로
dp[3][2] = min(dp[2][1], dp[2][2], dp[3][1]) = min(0, 1, 1) + 1 = 0 + 1 = 1이 된다.
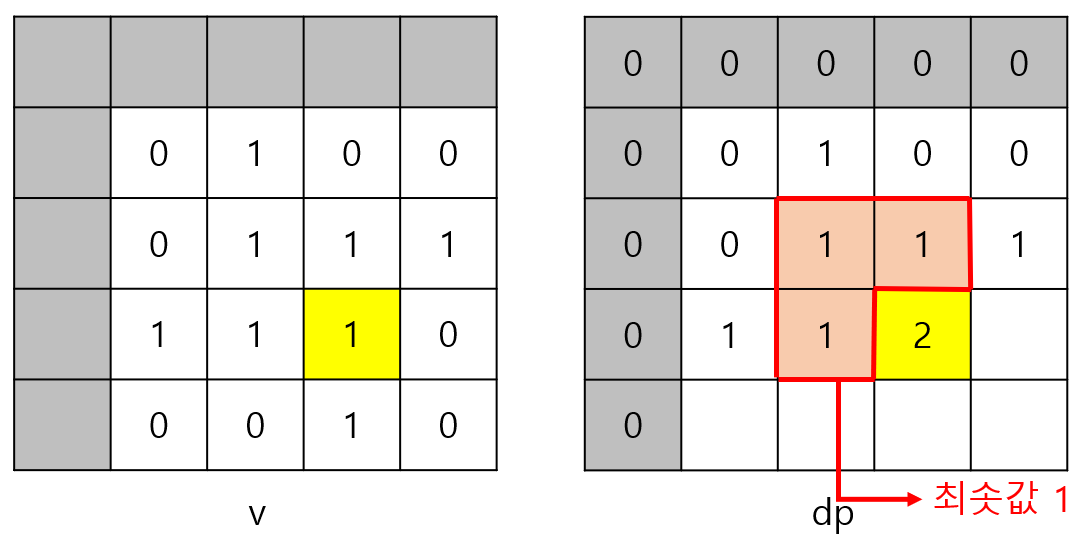
i = 3, j = 3일 때는 dp[2][2], dp[2][3], dp[3][2]의 최솟값이 1이므로
dp[3][3] = min(dp[2][2], dp[2][3], dp[3][2]) = min(1, 1, 1) + 1 = 1 + 1 = 2가 된다.
i = 3, j = 4일 때는 v[3][4]이 0이므로 dp[3][4]도 0이다.
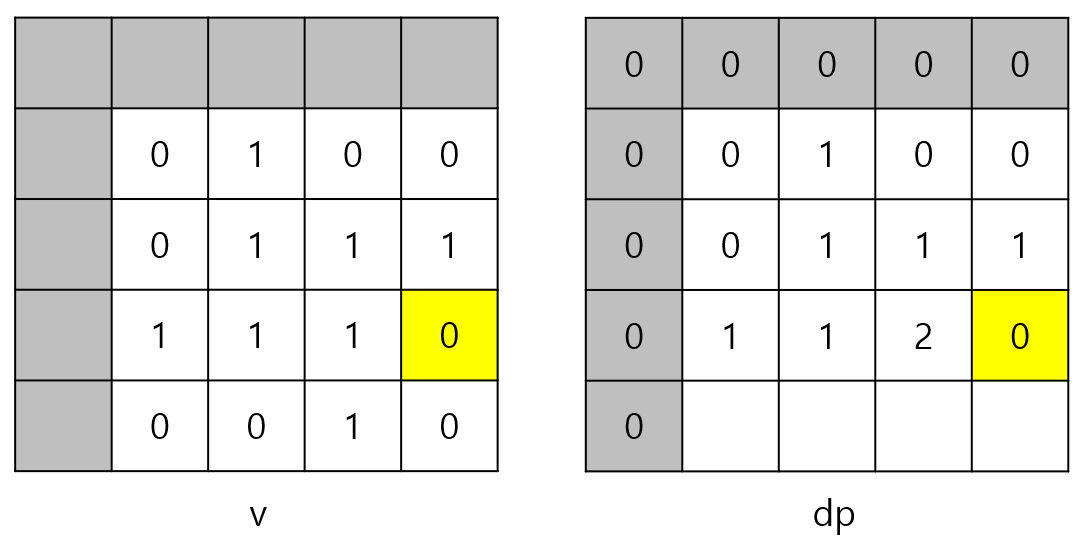
i = 4, j = 1일 때는 v[4][1]이 0이므로 dp[4][1]도 0이다.

i = 4, j = 2일 때는 v[4][2]이 0이므로 dp[4][2]도 0이다.
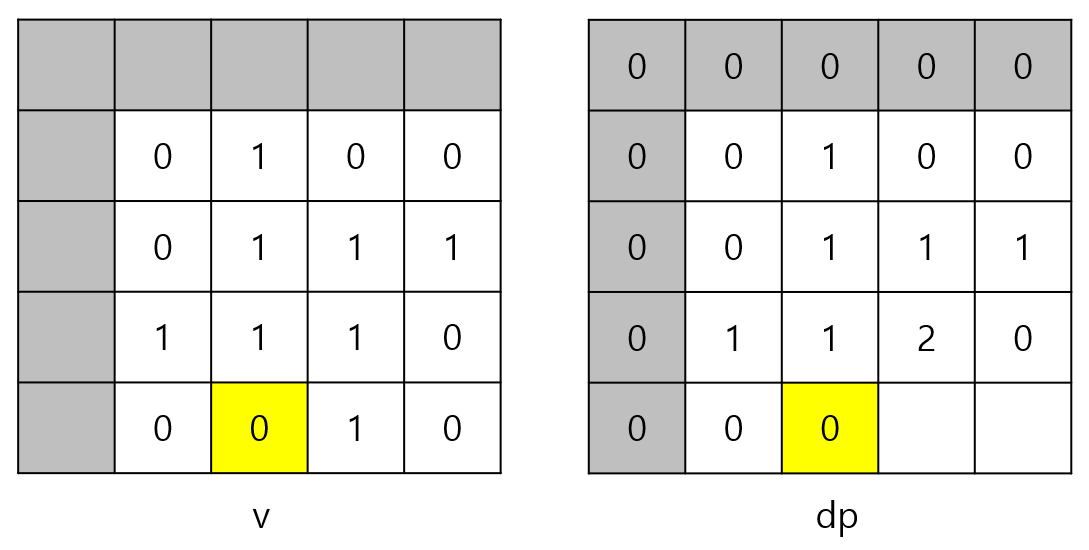
i = 4, j = 3일 때는 dp[3][2], dp[3][3], dp[4][2]의 최솟값이 0이므로
dp[4][3] = min(dp[2][2], dp[2][3], dp[3][2]) = min(1, 2, 0) + 1 = 0 + 1 = 1이 된다.

i = 4, j = 4일 때는 v[4][4]이 0이므로 dp[4][4]도 0이다.

이렇게 dp를 완성했으면 dp를 돌면서 최댓값을 찾으면 그것이 1로 만들 수 있는 가장 큰 정사각형의 한 변의 길이이다.
우리가 출력해야 하는 것은 가장 큰 정사각형의 넓이이므로 한 변의 길이의 제곱을 하면 된다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
cin.tie(NULL);
ios::sync_with_stdio(false);
int n, m;
cin >> n >> m;
vector<vector<char>> v(n + 1, vector<char>(m + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> v[i][j];
}
}
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (v[i][j] == '1') {
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
else {
dp[i][j] = 0;
}
}
}
int maxLength = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (dp[i][j] > maxLength) {
maxLength = dp[i][j];
}
}
}
cout << maxLength * maxLength;
return 0;
}